
A first-order mathematical model for a neuron could be this

where incoming connections are represented by input lines with an associated weight. The neuron in itself only doing accumulation and multiplication for each incoming pulses from each connection.
When a pulse comes from a connection, it is first multiplied by a number
called the weight of the connection which assignss a certain importance to
the connection (identical to the largeness of a biological dentrite), and
then accumulates the overall result, passing the value through a threshold
which emits a pulse when a certain value is reached.
The output of the threshold stage is in turn connected to the inputs to several other neurons,
which forms a complete network.
Unfortunately, it is difficult to apply even this simple mathematical to practical computing and signal processing applications, since the signals transmitted through biological neurons are in the form of pulses. Instead, we adopt a further simplification - ignoring the timing function of a biological neural network altogether, instead simply assuming that a set of real numbers are fed in, and a single real number is generated at the output.
So, can we, in practice, use real input and output numbers to model the
transactions between the different neurons?
The answer is definitively yes.
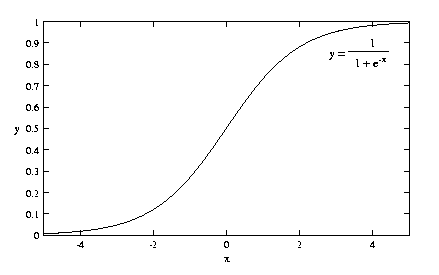
Instead of a biological threshold function, we use a mathematical
funtion such as the sigmoid function (1/(1 + exp (-x)), arctangent, arcsine,
etc. These functions should be smooth and continuous (i.e. you should not
use a piecewise linear or step function) and have an absolute upper and
lower limit.
They should also be differentiable. The above expressions also
have the convenient property that their derivative can be re-written in
terms of the function itself, which you will see improves the efficiency of
the network.
The sigmoid function is one of the most widely used node transfer functions, and is illustrated below:
| Previous | Contents | Next |